Преобразование Фурье
Опубликовано 26.08.2010
Ведущий Филипп Болгов
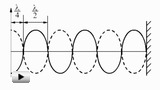
Почти каждый аудиолюбитель даже не будучи математиком, наверняка слышал о так называемом преобразовании Фурье, FFT, DFT и т.д. А все потому, что именно это преобразование лежит в основе спектрального анализа, который в свою очередь является одной из базисных вещей в эквализации и синтезе звука ...